So you want to solve a maze and could use some extra help. Or, more likely you are writing a computer program and want to know what options you have to solve a maze. I will take you through 8 popular maze solving methods and then discuss some of the the other most common everyday ways of solving mazes people use and give you some cheat codes. Here is what you can expect:
8 MAZE SOLVING METHODS
4 METHODS FOR PHYSICAL MAZES SOLVED FROM THE INSIDE
4 METHODS FOR MAZES VIEWED FROM ABOVE
5 COMMON MAZE SOLVING OPTIONS
2 CHEAT CODES TO SOLVE MAZES
2 INTERESTING MAZE SOLUTIONS
8 MAZE SOLVING METHODS
Let’s start with 4 methods used for physical mazes, like a hedge or corn maze, where you do not know what the maze looks like, i.e. you are a traveler in a maze looking to find the exit or goal.
Random Mouse Method - Very basic way to solve a maze and probably the way you typically do it. Starting walking, and randomly pick a direction at each intersection you reach. Nothing fancy, and not efficient, but works eventually. Also works for regular mazes you see from above - and probably how you solve most puzzle mazes.
Wall Follower Method - Well known way to solve a maze where you follow a wall consistently through a maze until you solve it. It can be a left handed or a right handed method, but once you choose your side you must stick with it ! To use this the maze must be simply connected, meaning it has no loops and all walls are attached to the outer walls of the maze.
Pledge Algorithm Method - A wall following method that can deal with disjointed walls. It involves counting turns you make (clockwise turn is positive, counter-clockwise turn is negative) and making decisions based on getting the number back to zero. Here are rules to follow to use it in practice:
Start at the entrance of the maze.
Move forward until a wall is encountered.
Follow the wall on the right-hand side until you reach the exit.
If you encounter a disjoint wall, you should turn left and continue following the wall on its right-hand side. How do you know you have a disjointed wall ? You arrive back at the same spot in a disjointed wall (a loop).
If you return to the starting point without finding the exit, turn around and follow the wall on its left-hand side until it reaches a new path. Then, it should follow the wall on its right-hand side again.
Repeat steps 3-5 until you reach the exit.
Trémaux's Algorithm - Uses a set of rules to solve a maze:
If you visit a junction with new paths, pick one at random.
Cross it out as you explore.
If you reach a dead end, retrace your steps to the last junction with unexplored paths and choose another path.
If you reach a junction with all paths already explored, retrace your steps to the last junction with unexplored paths and choose another path.
The following 4 methods of solving a maze are useful for typical puzzle mazes where you can see the complete maze from above:
Reverse Solve (Dead-end filling) - In this method you start at a known dead end and color in the pathway until you reach a junction. Eventually this process leads to a maze completely filled in expect for the correct pathway ! I like to use this for hidden message mazes !
Recursive algorithm - Math, coding. That is where this algorithm comes in. It uses X and Y values to check each spot inside a maze and determine if the space has been visited yet or not. It marks incorrect solutions as it goes and if it finds the correct pathway it marks in the X/Y values (pathway) of how it got there.
Maze-routing algorithm - Commonly used in chip design but can be used to solve a maze also. It is not something a person would use unless they coded it into a program. It works by finding the distant between any 2 points in the maze, blah, blah, blah, look you solved the maze !
Shortest Path Algorithms - A collection of many algorithms which all attempt to do the same thing - find the shortest path between 2 points - like let’s say the start and the goal ! While the details of this set of algorithms may not be for the average person to use to solve a maze, be glad it is used whenever you need directions between 2 points (Google Maps !, etc.)
Now let’s look more specifically at real world examples and the methods most people actually use for puzzle mazes. What method do you use to solve drawn mazes ?
5 COMMON MAZE SOLVING OPTIONS
With a writing utensil - probably the most common way to solve a drawn maze. You have a maze printed out or in a book in front of you and you grab a pen or pencil and solve using it. Makes the maze a one time use unless you have an eraser that does a good job and doesn’t harm the paper too much
With your finger - you use your finger as a guide to work your way through the maze and solve it. This method allows multiple people to solve the same maze
With your eyes - my personal most common maze solving method. Works for most maze types, although you need to add in a more comprehensive method for any spiral maze.
Reverse fill with a writing utensil - a method I used to use because I liked the way it looked. You use a pen / pencil and start at dead ends, filling each in until you reach a new branch. Eventually this leaves only the correct path NOT filled in, creating a reverse solve !
Of course online puzzles and mazes will use a combination of arrow keys or your mouse to solve a maze.
2 CHEAT CODES TO SOLVE MAZES
Solve it in Reverse - if a maze is giving you trouble, try solving it in reverse. Most mazes are mush easier this way since the maker of the maze likely designed it specifically to be solved in the Start to Goal direction. Of course some maze designers take this method into account and design difficulty in both directions ! These are called Dual entrance/exit mazes and you can learn how to make on and see examples of them here.
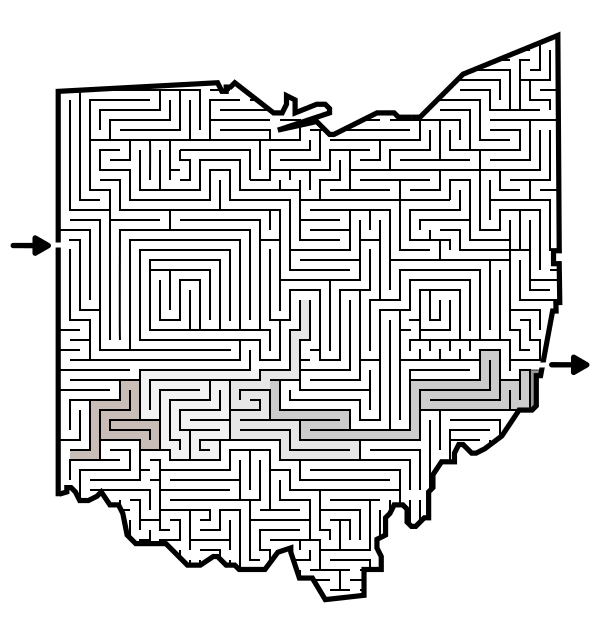
Middle Marking - This is what I call it. Before starting the maze pick a central spot in the maze and follow it until you reach a dead end. Color out that dead end. Choose the spot directly to the right of that spot and do the same. Repeat. The goal is to block out one side of the maze as unpassable by cutting it in half. Can also be done north/south. Here is an example where I repeated this 5 times (using 5 different shades of grey) and cut off the bottom half of the maze as a possibility. If I wanted to continue using this method I would start at the northern border and work my way down until I found the passable pathway !
Those are 15 ways to solve a maze. Now let’s look at some fun things to think about as a maze designer !
INTERESTING MAZE SOLUTIONS
If you like to design mazes I want to show you 2 fun ways to create maze solutions. Each can be used to add some fun to solving mazes.
Hidden Message Mazes - A maze that looks normal, but the solution has a message for the solver.
Here are 2 blog posts where I show you how to make your own (2 different types):
How to Make A Hidden Message Maze
How to Make a Hidden Message Trail Maze
And of course I made some templates (4 different) to help you make “mazed” letters if you are interested in creating your own mazes:
Hidden Message Maze Letter Design templates
Here is an example of a hidden message maze. See if you can figure out what it says before scrolling down:
Did you get it ? If you enjoy that challenge, check out Hidden Message Challenge - Part 1, or if you want to try some in Spanish: Desafío Laberinto de mensajes ocultos. You can also do this in regular mazes. like my maze of Monte Alban in Mexico.
Creative Maze Solutions
I find it hard to define this even though I have a great example of it.
My maze of the Museo Soumaya. Well, because I gave it a creative solution and that solution is even more hidden than a typical maze I make. I dare say it is completely hidden ! Let’s look at the maze. Do you see the answer ? You don’t.
To download the maze and solve it yourself check out the Museo Soumaya page here. Or just watch the solution on my YouTube channel below. When do you figure out the surprise ?
Happy